Type:	Package
Title:	Causal Effect for Population Attributable Fractions (PAF)
Version:	1.2.5
Date:	2022-08-18
Description:	Calculates population attributable fraction causal effects. The 'causalPAF' package contains a suite of functions for causal analysis calculations of population attributable fractions (PAF) given a causal diagram which apply both: Pathway-specific population attributable fractions (PS-PAFs) O’Connell and Ferguson (2022) <doi:10.1093/ije/dyac079> and Sequential population attributable fractions Ferguson, O’Connell, and O’Donnell (2020) <doi:10.1186/s13690-020-00442-x>. Results are presentable in both table and plot format.
License:	GPL-2 | GPL-3 [expanded from: GPL (≥ 2)]
URL:	https://github.com/MauriceOConnell/causalPAF
BugReports:	https://github.com/MauriceOConnell/causalPAF/issues
Depends:	R (≥ 2.10)
Imports:	checkmate, dagitty, dplyr, forestplot, ggdag, ggplot2, grid, gridExtra, magrittr, MASS, reshape2, rlist, splines, stats, utils
Suggests:	spelling
Config/testthat/edition:	3
Encoding:	UTF-8
Language:	en-US
LazyData:	true
RoxygenNote:	7.2.1
NeedsCompilation:	no
Packaged:	2022-08-19 23:16:50 UTC; mauriceoconnell
Author:	Maurice O'Connell [aut, cph, cre], John Ferguson [aut, cph]
Maintainer:	Maurice O'Connell <maurice.oconnell2@gmail.com>
Repository:	CRAN
Date/Publication:	2022-08-19 23:30:02 UTC

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome

Description

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome

Usage

addInSplinesTo_in_out(
  in_outDAG,
  splinesVariables,
  in_outDAG_SplinesRemoved,
  Splines_outlist_Var,
  splinesDefinedIn_in_outDAG,
  count,
  Subset_adjustmentSet
)

Arguments

Value

Returns in_outDAG with spline variables included

Evaluates Total PAF, Direct PAF, Indirect PAF and Path Specific PAF for a user inputted number of bootstraps and integral simulations

Description

Evaluates Total PAF, Direct PAF, Indirect PAF and Path Specific PAF for a user inputted number of bootstraps and integral simulations

Usage

causalPAFplot(
  dataframe,
  exposure = "phys",
  mediator = c("subhtn", "apob_apoa", "whr"),
  response = "case",
  response_model_mediators = list(),
  response_model_exposure = list(),
  in_outArg,
  Splines_outlist = list(),
  splinesDefinedIn_in_outDAG = list(),
  model_listArg = list(),
  weights = 1,
  NumBootstrap,
  NumSimulation,
  plot = "bar",
  fill = "skyblue",
  colour = "orange",
  addCustom = FALSE,
  custom = ""
)

Arguments

Value

Prints a forest plot or a bar chart with error bars of the 5 results for each mediator. The 5 results are:(1)Total Population Attributable Fraction (PAF),(2)Direct Effect Population Attributable Fraction (PAF) using alternative definition, (3)Indirect Effect Population Attributable Fraction (PAF) using alternative definition, (4)Path Specific Population Attributable Fraction (PAF), (5)Overall Direct Population Attributable Fraction (PAF)

Examples

# Loads some data (fictional Stroke data from the package 'causalPAF')
# In this example, we use a small data set called 'strokedata_smallSample' consisting of 5,000
# rows of fictional patient data. For more accurate results, a larger data set is available
# called 'strokedata'which contains 16,623 rows of fictional patient data. The methodology
# applied in the 'causalPAF' package is more accurate the larger the dataset. To use the larger
# 'strokedata' dataset, simply call
# stroke_reduced <- strokedata
stroke_reduced <- strokedata_smallSample

# Just shortening the name of a variable, "apob_apoa", to "apb" so the R code
# in document example is not truncated.
stroke_reduced$apb  <- stroke_reduced$apob_apoa

# The data should contain a column of weights for case control matching.
# strokedata$weights
# Weigths are not needed for cohort/cross sectional designs.

# The data should have reference levels of all risk factors already set.
# This can be done as follows but has already been applied to the data so is not run here:
# levels(stroke_reduced$htnadmbp) <- c(0, 1)
# stroke_reduced$subhtn <-  factor(stroke_reduced$subhtn,levels=c(1, 2))
# levels(stroke_reduced$nevfcur) <- c(1, 2)
# stroke_reduced$global_stress2  <- factor(stroke_reduced$global_stress2,levels=c(1,2))
# levels(stroke_reduced$whrs2tert) <- c(1, 2, 3)
# levels(stroke_reduced$phys) <- c(2, 1)
# levels(stroke_reduced$alcohfreqwk) <- c(1, 2, 3)
# stroke_reduced$dmhba1c2 <- factor(stroke_reduced$dmhba1c2,levels=c(1,2))
# stroke_reduced$cardiacrfcat <- factor(stroke_reduced$cardiacrfcat,levels=c(1,2))
# levels(stroke_reduced$ahei3tert) <- c(3,2,1)
# levels(stroke_reduced$apob_apoatert) <- c(1,2,3)

# The 'causalPAF' package assumes the data is either complete case data or that missing data
# analysis has already been performed.

# Next, define the causal structure or directed acyclic graph (DAG) of the causal Bayesian
# network defined by the data. We list the parents of each exposure or risk factor or outcome
# in a vector as follows:

# Note it is important that the order at which the variables are defined is such that all
# parents of that variable are defined before it. Please refer to the figure of the causal
# Bayesian network (with both direct and indirect effects) defined earlier as an example of this
# order.

in_phys <- c("subeduc","moteduc","fatduc")
in_ahei <- c("subeduc","moteduc","fatduc")
in_nevfcur <- c("subeduc","moteduc","fatduc")
in_alcohfreqwk <- c("subeduc","moteduc","fatduc")
in_global_stress2 <- c("subeduc","moteduc","fatduc")
in_subhtn <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
               "global_stress2")
in_apob_apoa <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2")
in_whr <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
            "global_stress2")

# Note splines can be fitted within the causal structure as shown below especially if splines
# are to be used in the fitted models.
# It is important that splines of parent variables are "typed" or "spelt" consistently
# (including spaces) throughout as 'causalPAF' can fit models automatically provided variables are
# spelt consistently. Also if a parent variable is a spline it should be defined in spline
# format in all occurences of the parent variable.
in_cardiacrfcat <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                     "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn")
in_dmhba1c2 <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                 "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn")
in_case <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
             "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn","cardiacrfcat","dmhba1c2")

# Then we define a two dimensional list consisting of
# 1. inlist i.e. a list of the parents of each variable of interest corresponding to its column
# name in the data. Splines should be included here if they are to be modelled as splines.
# 2. outlist i.e. a list of each variable of interest corresponding to its column name in the
# data. Splines should not be input here, only the column names of the variables of interest in
# the data.
# Again the order is such that each variable is defined after all its parents.

in_out <- list(inlist=list(in_phys,in_ahei,in_nevfcur,in_alcohfreqwk,in_global_stress2,
               in_subhtn,in_apob_apoa,in_whr,in_cardiacrfcat,in_dmhba1c2,in_case),
               outlist=c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2","subhtn",
                         "apb","whr","cardiacrfcat","dmhba1c2","case"))

# If splines are to be used for variables listed in in_out$outlist, then the splines should be
# defined in the same order as variables appear in in_out$outlist as follows. It is necessary to
# list variables in in_out$outlist without splines if no spline is to be applied.
# It is important that Splines_outlist is defined in the following format
# list(c("splinename1","splinename2","splinename3")) for the package to be applied correctly.
# And Splines_outlist should not be an empty list(). If there are no splines it should be
# defined the same as in_out[[2]] and in the same order as variables defined in_out[[2]].
Splines_outlist = list( c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2","subhtn",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","cardiacrfcat","dmhba1c2","case") )

# To fit these models to case control data, one needs to perform weighted maximum likelihood
# estimation to imitate estimation using a random sample from the population. We chose weights
# of 0.0035 (for each case) and 0.9965 (for each control), reflective of a yearly incidence of
# first ischemic stroke of 0.35%, or 3.5 strokes per 1,000 individuals. These weights were
# chosen according to average incidences across country, age, group and gender within
# INTERSTROKE according to the global burden of disease.
w <- rep(1,nrow(stroke_reduced))
w[stroke_reduced$case==0] <- 0.9965
w[stroke_reduced$case==1] <- 0.0035

# It is important to assign stroke_reduced$weights to the updated weights defined in w.
# Otherwise if stroke_reduced$weights <- w is not set, the alternative weights supplied in the
#  fictional data will be used. In this case, we want to use weigths as defined in w.
stroke_reduced$weights <- w

#The checkMarkovDAG() function in the 'causalPAF' package should be used before running
# causalPAFplot() to ensure:
#1. The causal Markov condition holds for the causal structure defined in the variable in_out.
#2. The variables in in_out are listed in the order so that no variable is defined before a
# parent or direct cause. Note: if this order does not hold, checkMarkovDAG() will automatically
# reorder the variables in, in_out, provided it is a Markov DAG.

#The causal analysis requires that the causal structure is a Markov DAG. The Causal Markov (CM)
# condition states that, conditional on the set of all its direct causes, a node is independent
# of all variables which are not direct causes or direct effects of that node. In the event that
# the structure of a Bayesian network accurately depicts causality, the two conditions are
# equivalent. However, a network may accurately embody the Markov condition without depicting
# causality, in which case it should not be assumed to embody the causal Markov condition.

# in_out is as defined above and input into this code.

if(checkMarkovDAG(in_out)$IsMarkovDAG & !checkMarkovDAG(in_out)$Reordered){
  print("Your in_out DAG is a Markov DAG.")
  } else if( checkMarkovDAG(in_out)$IsMarkovDAG & checkMarkovDAG(in_out)$Reordered ) {

      in_out <- checkMarkovDAG(in_out)[[2]]

          print("Your in_out DAG is a Markov DAG.The checkMarkovDAG function has reordered your
               in_out list so that all parent variables come before descendants.")
          } else{ print("Your ``in_out'' list is not a Bayesian Markov DAG so the methods in the
                        'causalPAF' package cannot be applied for non Markov DAGs.")}

# The pointEstimate() function evaluates Point Estimates for Total PAF, Direct PAF, Indirect PAF
# and Path Specific PAF for a user inputted number of integral simulations. There is no bootstrap
# applied in this fucntion.
# Since bootstraps are not applied, the pointEstimate() function will run quicker than the
# alternative causalPAFplot() function which calculates bootstrap estimates which can take
# longer to run.


         pointEstimate(dataframe = stroke_reduced,
                       exposure="phys",
                       mediator=c("subhtn","apb","whr"),
                       response="case",
                       response_model_mediators = list(),
                       response_model_exposure = list(),
                       in_outArg = in_out,
                       Splines_outlist = Splines_outlist,
                       splinesDefinedIn_in_outDAG = TRUE,
                       model_listArg = list(),
                       weights = w,
                       NumSimulation = 3,
                       addCustom = TRUE,
                       custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)")



# The causalPAFplot() function will perform Pathway Specific Population Attributable Fraction
# (PSPAF) calculations and output results based on an exposure, mediators and response input
# by the user according to the columns names of these variables defined in the dataframe.

# Setting model_listArg, response_model_mediators and response_model_exposure by default to an
# empty list will instruct the 'causalPAF' package to fit these models automatically based on the
# causal DAG supplied in the in _outArg. Alternatively the user can supply their custom fitted,
# model_listpop, response_model_mediators and response_model_exposure which should be consistent
# with the causal structure.

# Note we fit a custom interaction for the outcome (or case or response) regression
# ( custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)") ). Care should be taken that the
# customised regression should not contain variables that might affect the causal interpretation
# of the regression e.g. in this case we have used baseline confounders (i.e. regionn, eage and
# esex) with interactions and splines. In general, using baseline confounders in custom should
# not affect any causal interpretations whereas using variables far ``downstream'' might block
# causal pathways. The user is required to apply discretion in using ``addCustom'' and
# ``Custom'' in ensuring a causal interpretation remains. If no customisation is required the
# user can input addCustom = FALSE and custom = "" which is the default setting.

# Finally we call the causalPAFplot function for the pathway specific PAF calculations as
# follows:
# For greater accuracy a larger number of bootstraps (e.g. 200) and larger number of simulations
# (e.g. 1000) should be run. However, this will increase the run time greatly.

         causalPAFplot(dataframe = stroke_reduced,
                       exposure="phys",
                       mediator=c("subhtn","apb","whr"),
                       response="case",
                       response_model_mediators = list(),
                       response_model_exposure = list(),
                       in_outArg = in_out,
                       Splines_outlist = Splines_outlist,
                       splinesDefinedIn_in_outDAG = TRUE,
                       model_listArg = list(),
                       weights = w,
                       NumBootstrap = 2,
                       NumSimulation = 2,
                       plot = "bar",
                       fill= "skyblue",
                       colour="orange",
                       addCustom = TRUE,
                       custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)")


# The causalPAFplot function below has response_model_mediators, response_model_exposure and
# model_listArg pre fit. This allows the user to apply customised regressions instead of the
# default setting above, where the 'causalPAF' R package fitted these regressions automatically
# based on the causalDAG defined in in_outArg.

# Libraries must be loaded if fitting models outside of the 'causalPAF' R package.

library(MASS)
library(splines)


# Next we fit the, response_model_mediators and response_model_exposure, models outside of the
# 'causalPAF' package as an input into the package.

# It is important that response_vs_mediator is a list and it must be the same length as the
# parameter, mediator, i.e. length( response_vs_mediator ) == length( mediator). In this
# example, mediator=c("subhtn","apb","whr") so length( mediator) is 3, so we create a list
# with three models for "subhtn","apb" and "whr" respectively in that order. Note in this
# example, the model is the same for each mediator, but it must still be input 3 times within
# the list as follows:

response_vs_mediator <-  list(
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +subeduc+moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ),
# "subhtn" mediator model
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +  subeduc+ moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ),
# "apob_apoa" mediator model name shoretd to "apb"
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +  subeduc+ moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ) )
 # "whr" mediator model


# Next we fit a customised response_model_exposure model rather than allowing the package fit it
# automatically as shown previously. This must be a list of length 1.

response_vs_phys <- list(glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)+subeduc+moteduc+
fatduc+ phys+ ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2",data = stroke_reduced,
family='binomial',w= stroke_reduced$weights) )


# model_listArg is a list of models fitted for each of the variables in in_out$outlist based on
# its parents given in in_out$inlist. By default this is set to an empty list. Alternatively the
# user can supply their custom fitted, model_listpop, which should be consistent with the causal
# structure. model_listArg is defined earlier in this tutorial.
# Note it is important that model_listArg is defined as a list and in the same order and length
# as the variables defined in in_outArg[[2]].


model_listArgFit <- list(glm(formula = phys ~ subeduc + regionnn7 * ns(eage, df = 5) +
esex * ns(eage, df = 5) + moteduc + fatduc, family = "binomial", data = stroke_reduced,
 weights = weights), # model 1 phys
polr(formula = ahei3tert ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, data = stroke_reduced, weights = weights), # model 2 ahei3tert
glm(formula = nevfcur ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, family = "binomial",data = stroke_reduced, weights = weights),
# model 3 nevfcur
polr(formula = alcohfreqwk ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc, data = stroke_reduced,weights = weights), # model 4 alcohfreqwk
glm(formula = global_stress2 ~ subeduc + regionnn7 * ns(eage,df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, family = "binomial",data = stroke_reduced, weights = weights),
# model 5 global_stress2
glm(formula = subhtn ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2,family = "binomial",
data = stroke_reduced, weights = weights), # model 6 subhtn
lm(formula = apb ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2,
data = stroke_reduced,weights = weights), # model 7 apob_apoa name shorted to "apb"
lm(formula = whr ~ subeduc + regionnn7 * ns(eage, df = 5) + esex *ns(eage, df = 5) + moteduc +
fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2, data = stroke_reduced,
weights = weights), # model 8 whr
glm(formula = cardiacrfcat ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn,
family = "binomial",data = stroke_reduced, weights = weights), # model 9 cardiacrfcat
glm(formula = dmhba1c2 ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn,
family = "binomial",data = stroke_reduced, weights = weights), # model 10 dmhba1c2
glm(formula = case ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) + moteduc +
fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn +
cardiacrfcat +dmhba1c2, family = "binomial", data = stroke_reduced, weights = weights)
# model 11 case
)


# For greater accuracy a larger number of bootstraps (e.g. 200) and larger number of simulations
# (e.g. 1000) should be run. However, this will increase the run time greatly.
        causalPAFplot(dataframe = stroke_reduced,
                      exposure="phys",
                      mediator=c("subhtn","apb","whr"),
                      response="case",
                      response_model_mediators = response_vs_mediator,
                      response_model_exposure = response_vs_phys,
                      in_outArg = in_out,
                      Splines_outlist = Splines_outlist,
                      splinesDefinedIn_in_outDAG = TRUE,
                      model_listArg = model_listArgFit,
                      weights = w,
                      NumBootstrap = 2,
                      NumSimulation = 2,
                      plot = "bar",
                      fill= "skyblue",
                      colour ="orange" )

Checks if the causal DAG satisfies the Markov condition

Description

The functions checks if the Markov condition holds for the Directed Acyclic Graph (DAG) defined. Sometimes called the Markov assumption, is an assumption made in Bayesian probability theory, that every node in a Bayesian network is conditionally independent of its nondescendants, given its parents. In other words, it is assumed that a node has no bearing on nodes which do not descend from it. This is equivalent to stating that a node is conditionally independent of the entire network, given its Markov blanket. The related Causal Markov condition states that, conditional on the set of all its direct causes, a node is independent of all variables which are not direct causes or direct effects of that node.

Usage

checkMarkovDAG(in_out)

Arguments

Value

Examples

# Loads some data (fictional Stroke data from the package 'causalPAF')
# In this example, we use a small data set called 'strokedata_smallSample' consisting of 5,000
# rows of fictional patient data. For more accurate results, a larger data set is available
# called 'strokedata'which contains 16,623 rows of fictional patient data. The methodology
# applied in the 'causalPAF' package is more accurate the larger the dataset. To use the larger
# 'strokedata' dataset, simply call
# stroke_reduced <- strokedata
stroke_reduced <- strokedata_smallSample

in_phys <- c("subeduc","moteduc","fatduc")
in_ahei <- c("subeduc","moteduc","fatduc")
in_nevfcur <- c("subeduc","moteduc","fatduc")
in_alcohfreqwk <- c("subeduc","moteduc","fatduc")
in_global_stress2 <- c("subeduc","moteduc","fatduc")
in_htnadmbp <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                 "global_stress2")
in_apob_apoatert <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                      "global_stress2")
in_whrs2tert <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2")
in_cardiacrfcat <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                     "global_stress2", "apob_apoatert","whrs2tert","htnadmbp")
in_dmhba1c2 <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2", "apob_apoatert","whrs2tert","htnadmbp")
in_case <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
"global_stress2", "apob_apoatert","whrs2tert","htnadmbp","cardiacrfcat","dmhba1c2")

in_out <- list(inlist=list(in_phys,in_ahei,in_nevfcur,in_alcohfreqwk,in_global_stress2,
               in_htnadmbp, in_apob_apoatert,in_whrs2tert,in_cardiacrfcat,
               in_dmhba1c2,in_case),
               outlist=c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2",
                         "htnadmbp","apob_apoatert", "whrs2tert","cardiacrfcat",
                         "dmhba1c2","case"))


if(checkMarkovDAG(in_out)$IsMarkovDAG & !checkMarkovDAG(in_out)$Reordered){
  print("Your in_out DAG is a Markov DAG.")
} else if( checkMarkovDAG(in_out)$IsMarkovDAG & checkMarkovDAG(in_out)$Reordered ) {

  in_out <- checkMarkovDAG(in_out)[[2]]

  print("Your in_out DAG is a Markov DAG.The checkMarkovDAG function has reordered your
          in_out list so that all parent variables come before descendants.")
} else{ print("Your ``in_out'' list is not a Bayesian Markov DAG so the methods in the
               'causalPAF' package cannot be applied for non Markov DAGs.")}

Makes Formula

Description

Given a causal

Usage

do_sim(model, dataframe)

Arguments

Value

Examples

## Not run: 
# I don't want you to run this

## End(Not run)

Simulates a Fitted Model for a Mediator or Exposure or Risk Factor Allowing for Potential Outcomes in Causal Analysis

Description

A fitted model for a mediator or exposure or risk factor can be simulated given values of the other risk factors or exposure saved in the data frame current_mat. This allows for potential outcomes to be measured for causal analysis. For example, for an outcome Y_{A,M} with exposure A and mediators M_{1}, M_{3}, \dots M_{K} the function can measure potential outcomes such as Y_{A=0,M_{1},M_{2},M_{3}} or Y_{A=0,M_{1},M_{2}=0,M_{3}=0} when there are three mediators. The model can be either a binary, continuous or an ordered factor response model.

Usage

do_sim_sequentialPAF(colnum, current_mat, model)

Arguments

Value

Examples

## Not run: 
# I don't want you to run this

## End(Not run)

Evaluates and Makes Formula for regression of exposure or risk factor or outcome on its parents in a causal Bayesian network directed acyclic graph.

Description

Evaluates and Makes Formula for regression of exposure or risk factor or outcome on its parents in a causal Bayesian network directed acyclic graph. Given a causal Bayesian network, directed acyclic graph (DAG) where arrows representing causal dependencies between confounders, risk factors,exposure and disease, together with a sensible probability distribution on the graph that respects these causal dependencies. To consistently estimate causal effects that risk factors may have on each other and on disease, we need to make a strong no unmeasured confounding assumption: that is common causes of nodes in the graph, which may be causes of two risk factors or a cause of risk factor and disease, are also included as nodes in the graph. Causal Bayesian networks have a local Markov property that the conditional probability distribution of any node X_j, given values for the other variables in the network, only depends on the values x_{pa_{j}} of the parent nodes.

Usage

eval_make_DAG(
  data,
  regressionExposure,
  regressionMediator,
  response,
  response_model_mediators,
  response_model_exposure,
  w
)

Arguments

Value

• regressionExposure_listReturn model list regressionExposure_listReturn

• regressionMediator_listReturn model list regressionMediator_listReturn

Evaluates and Makes Formula for regression of exposure or risk factor or outcome on its parents in a causal Bayesian network directed acyclic graph.

Description

Evaluates and Makes Formula for regression of exposure or risk factor or outcome on its parents in a causal Bayesian network directed acyclic graph. Given a causal Bayesian network, directed acyclic graph (DAG) where arrows representing causal dependencies between confounders, risk factors, exposure and disease, together with a sensible probability distribution on the graph that respects these causal dependencies. To consistently estimate causal effects that risk factors may have on each other and on disease, we need to make a strong no unmeasured confounding assumption: that is common causes of nodes in the graph, which may be causes of two risk factors or a cause of risk factor and disease, are also included as nodes in the graph. Causal Bayesian networks have a local Markov property that the conditional probability distribution of any node X_j, given values for the other variables in the network, only depends on the values x_{pa_{j}} of the parent nodes.

Usage

eval_make_formula(data, in_out, model_list, w, addCustom = FALSE, custom = "")

Arguments

Value

• model_listReturn[[1]] model list A

• model_listReturn[[2]] model list B

• model_listReturn[[3]] model list C

• model_listReturn[[4]] model list D

• model_listReturn[[5]] model list E

• model_listReturn[[6]] model list F

• model_listReturn[[7]] model list G

• model_listReturn[[8]] model list H

• model_listReturn[[9]] model list I

• model_listReturn[[10]] model list J

• model_listReturn[[11]] model list K

Calculation of Population Attributable Fraction (PAF), with a decomposition of the total PAF into direct and indirect components.

Description

Calculation of Population Attributable Fraction (PAF), with a decomposition of the total PAF into direct and indirect components. It performs one simulation which can be combined with a bootstrap approach to perform multiple simulations. If we think of Y_0 as the potential outcome for an individual if they were never exposed to the risk factor, can be directly interpreted as the relative change in disease prevalence if an exposure was absent from the population. Sjolander introduced the ideas of mediation into the literature for PAF, defining a decomposition of the total PAF into direct and indirect components: and 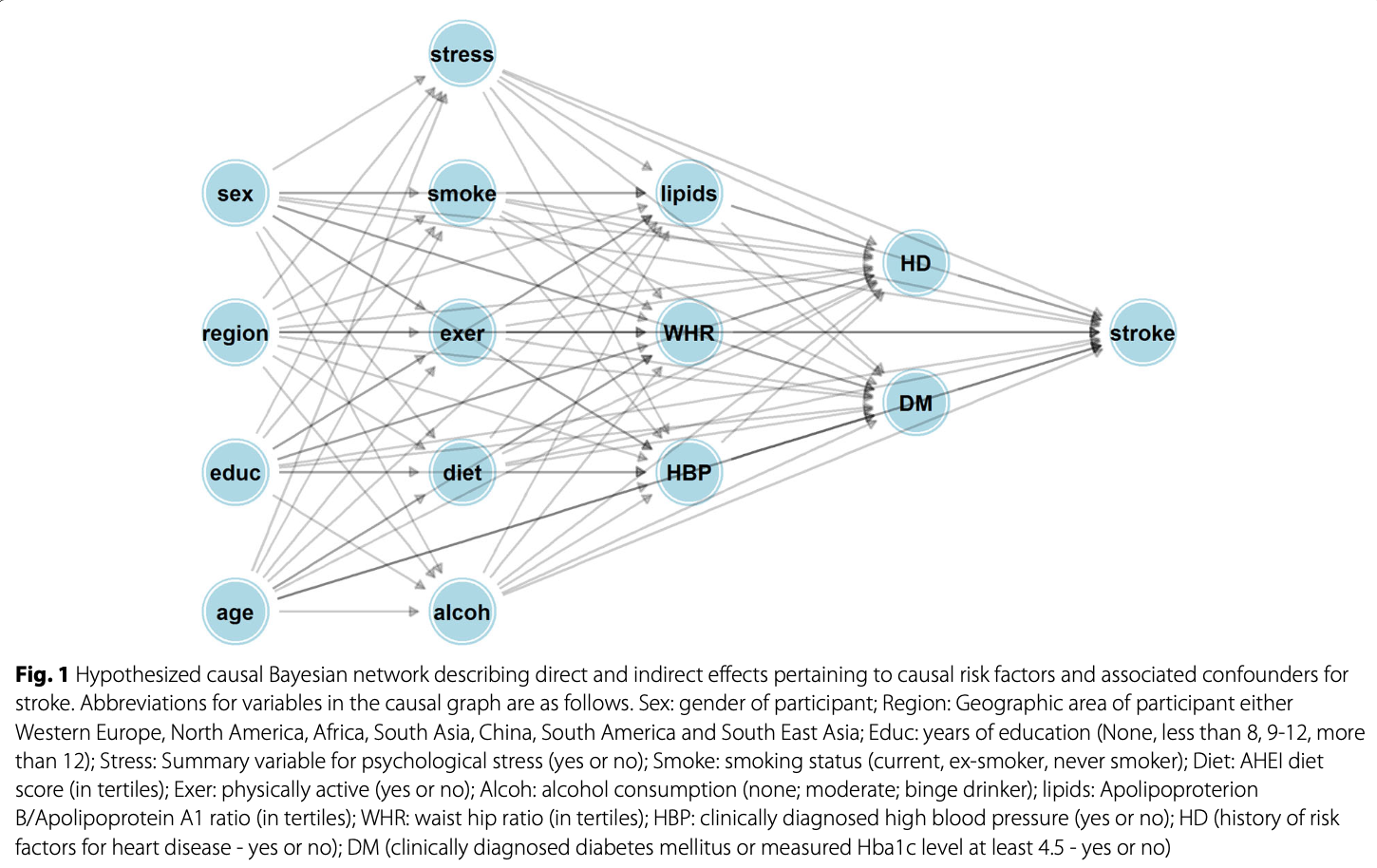options: width=100 alt="Causal Bayesian network DAG"

Usage

indirect_PAF_Sjolander_onesimulation(
  data_frame,
  exposure,
  mediator,
  response,
  mediator_model,
  response_model,
  response_model_2,
  weights
)

Arguments

Value

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome

Description

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome

Usage

make_DAG(
  in_outDAG,
  exposure,
  response,
  mediator,
  Splines_outlist_Var = list(),
  splinesDefinedIn_in_outDAG = list(),
  addCustomExposureAdjustmentSet = FALSE,
  customExposureAdjustmentSet,
  addCustomMediatorAdjustmentSet = FALSE,
  customMediatorAdjustmentSet
)

Arguments

Value

Returns DAG and adjustment set given exposure and outcome.

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome.

Description

Creates a DAG for input into package Dagitty to identify adjustmentSets given exposure and outcome. Splines are removed initially and then added back in. Adjustment sets populated by the user are updated with valid adjustment sets if necessary.

Usage

make_DAG_AdjustmentSets_in_out(
  in_outDAG,
  exposure,
  response,
  mediator,
  Splines_outlist_Var = list(),
  splinesDefinedIn_in_outDAG = list(),
  addCustomExposureAdjustmentSet = FALSE,
  customExposureAdjustmentSet,
  addCustomMediatorAdjustmentSet = FALSE,
  customMediatorAdjustmentSet
)

Arguments

Value

Returns DAG and adjustment set given exposure and outcome with spline variables included and updates any adjustment sets if necessary for valid adjustments.

Makes Formula for regression of exposure or risk factor or outcome on its parents in a causal Bayesian network directed acyclic graph.

Description

Given a causal Bayesian network, directed acyclic graph (DAG) where arrows representing causal dependencies between confounders, risk factors, exposure and disease, together with a sensible probability distribution on the graph that respects these causal dependencies. To consistently estimate causal effects that risk factors may have on each other and on disease, we need to make a strong no unmeasured confounding assumption: that is common causes of nodes in the graph, which may be causes of two risk factors or a cause of risk factor and disease, are also included as nodes in the graph. Causal Bayesian networks have a local Markov property that the conditional probability distribution of any node X_j, given values for the other variables in the network, only depends on the values x_{pa_{j}} of the parent nodes.

Usage

make_formula(in_vars, outvar, addCustom = FALSE, custom = "")

Arguments

Value

Calculation of Population Attributable Fraction (PAF), with a decomposition of the total PAF into direct and indirect components.

Description

Total PAF

Usage

overall_direct(
  data_frame,
  exposure,
  mediator,
  response,
  mediator_model,
  response_model,
  response_model_2,
  weights
)

Arguments

Value

Path specific population attributable fraction for a mediating pathway.

Description

Path specific population attributable fraction for a mediating pathway. This metric has several desirable properties. This is a kind of sequential PAF on pathways, but now corresponding to eliminating the mediating pathway first.

PAF_{A->M->Y} = (P(Y=1)-P(Y_{A,M_{0}}=1)/P(Y=1)

options: width=100 alt="Causal Bayesian network DAG"

Usage

path_specific_onesimulation(
  data_frame,
  exposure,
  mediator,
  response,
  mediator_model,
  response_model,
  response_model_2,
  weights
)

Arguments

Value

Evaluates Point Estimates for Total PAF, Direct PAF, Indirect PAF and Path Specific PAF for a user inputted number of integral simulations. There is no bootstrap applied in this function.

Description

Evaluates Total PAF, Direct PAF, Indirect PAF and Path Specific PAF for a user inputted number of bootstraps and integral simulations

Usage

pointEstimate(
  dataframe,
  exposure = "phys",
  mediator = c("subhtn", "apob_apoa", "whr"),
  response = "case",
  response_model_mediators = list(),
  response_model_exposure = list(),
  in_outArg,
  Splines_outlist,
  splinesDefinedIn_in_outDAG,
  model_listArg,
  weights = 1,
  NumSimulation,
  addCustom = FALSE,
  custom = ""
)

Arguments

Value

Estimates point estimates for 5 results that are:(1)Total Population Attributable Fraction (PAF),(2)Direct Effect Population Attributable Fraction (PAF) using alternative definition, (3)Indirect Effect Population Attributable Fraction (PAF) using alternative definition, (4)Path Specific Population Attributable Fraction (PAF), (5)Overall Direct Population Attributable Fraction (PAF)

Examples

# Loads some data (fictional Stroke data from the package 'causalPAF')
# In this example, we use a small data set called 'strokedata_smallSample' consisting of 5,000
# rows of fictional patient data. For more accurate results, a larger data set is available
# called 'strokedata'which contains 16,623 rows of fictional patient data. The methodology
# applied in the 'causalPAF' package is more accurate the larger the dataset. To use the larger
# 'strokedata' dataset, simply call
# stroke_reduced <- strokedata
stroke_reduced <- strokedata_smallSample

# Just shortening the name of a variable, "apob_apoa", to "apb" so the R code
# in document example is not truncated.
stroke_reduced$apb  <- stroke_reduced$apob_apoa

# The data should contain a column of weights for case control matching.
# strokedata$weights
# Weigths are not needed for cohort/cross sectional designs.

# The data should have reference levels of all risk factors already set.
# This can be done as follows  but has already been applied to the data so is not run here:
# levels(stroke_reduced$htnadmbp) <- c(0, 1)
# stroke_reduced$subhtn <-  factor(stroke_reduced$subhtn,levels=c(1, 2))
# levels(stroke_reduced$nevfcur) <- c(1, 2)
# stroke_reduced$global_stress2  <- factor(stroke_reduced$global_stress2,levels=c(1,2))
# levels(stroke_reduced$whrs2tert) <- c(1, 2, 3)
# levels(stroke_reduced$phys) <- c(2, 1)
# levels(stroke_reduced$alcohfreqwk) <- c(1, 2, 3)
# stroke_reduced$dmhba1c2 <- factor(stroke_reduced$dmhba1c2,levels=c(1,2))
# stroke_reduced$cardiacrfcat <- factor(stroke_reduced$cardiacrfcat,levels=c(1,2))
# levels(stroke_reduced$ahei3tert) <- c(3,2,1)
# levels(stroke_reduced$apob_apoatert) <- c(1,2,3)

# The 'causalPAF' package assumes the data is either complete case data or that missing data
# analysis has already been performed.

# Next, define the causal structure or directed acyclic graph (DAG) of the causal Bayesian
# network defined by the data. We list the parents of each exposure or risk factor or outcome
# in a vector as follows:

# Note it is important that the order at which the variables are defined is such that all
# parents of that variable are defined before it. Please refer to the figure of the causal
# Bayesian network (with both direct and indirect effects) defined earlier as an example of this
# order.

in_phys <- c("subeduc","moteduc","fatduc")
in_ahei <- c("subeduc","moteduc","fatduc")
in_nevfcur <- c("subeduc","moteduc","fatduc")
in_alcohfreqwk <- c("subeduc","moteduc","fatduc")
in_global_stress2 <- c("subeduc","moteduc","fatduc")
in_subhtn <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
               "global_stress2")
in_apob_apoa <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2")
in_whr <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
            "global_stress2")

# Note splines can be fitted within the causal structure as shown below especially if splines
# are to be used in the fitted models.
# It is important that splines of parent variables are "typed" or "spelt" consistently
# (including spaces) throughout as 'causalPAF' can fit models automatically provided variables are
# spelt consistently. Also if a parent variable is a spline it should be defined in spline
# format in all occurences of the parent variable.
in_cardiacrfcat <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                     "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn")
in_dmhba1c2 <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                 "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn")
in_case <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
             "global_stress2",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","subhtn","cardiacrfcat","dmhba1c2")

# Then we define a two dimensional list consisting of
# 1. inlist i.e. a list of the parents of each variable of interest corresponding to its column
# name in the data. Splines should be included here if they are to be modelled as splines.
# 2. outlist i.e. a list of each variable of interest corresponding to its column name in the
# data. Splines should not be input here, only the column names of the variables of interest in
# the data.
# Again the order is such that each variable is defined after all its parents.

in_out <- list(inlist=list(in_phys,in_ahei,in_nevfcur,in_alcohfreqwk,in_global_stress2,
               in_subhtn,in_apob_apoa,in_whr,in_cardiacrfcat,in_dmhba1c2,in_case),
               outlist=c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2","subhtn",
                         "apb","whr","cardiacrfcat","dmhba1c2","case"))

# If splines are to be used for variables listed in in_out$outlist, then the splines should be
# defined in the same order as variables appear in in_out$outlist as follows. It is necessary to
# list variables in in_out$outlist without splines if no spline is to be applied.
# It is important that Splines_outlist is defined in the following format
# list(c("splinename1","splinename2","splinename3")) for the package to be applied correctly.
# And Splines_outlist should not be an empty list(). If there are no splines it should be
# defined the same as in_out[[2]] and in the same order as variables defined in_out[[2]].
Splines_outlist = list( c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2","subhtn",
"ns(apb,knots=quantile(apb,c(.25,.5,.75)),Boundary.knots=quantile(apb,c(.001,.95)))",
"ns(whr,df=5)","cardiacrfcat","dmhba1c2","case") )

# To fit these models to case control data, one needs to perform weighted maximum likelihood
# estimation to imitate estimation using a random sample from the population. We chose weights
# of 0.0035 (for each case) and 0.9965 (for each control), reflective of a yearly incidence of
# first ischemic stroke of 0.35%, or 3.5 strokes per 1,000 individuals. These weights were
# chosen according to average incidences across country, age, group and gender within
# INTERSTROKE according to the global burden of disease.
w <- rep(1,nrow(stroke_reduced))
w[stroke_reduced$case==0] <- 0.9965
w[stroke_reduced$case==1] <- 0.0035

# It is important to assign stroke_reduced$weights to the updated weights defined in w.
# Otherwise if stroke_reduced$weights <- w is not set, the alternative weights supplied in the
#  fictional data will be used. In this case, we want to use weigths as defined in w.
stroke_reduced$weights <- w

#The checkMarkovDAG() function in the 'causalPAF' package should be used before running
# causalPAFplot() to ensure:
#1. The causal Markov condition holds for the causal structure defined in the variable in_out.
#2. The variables in in_out are listed in the order so that no variable is defined before a
# parent or direct cause. Note: if this order does not hold, checkMarkovDAG() will automatically
# reorder the variables in, in_out, provided it is a Markov DAG.

#The causal analysis requires that the causal structure is a Markov DAG. The Causal Markov (CM)
# condition states that, conditional on the set of all its direct causes, a node is independent
# of all variables which are not direct causes or direct effects of that node. In the event that
# the structure of a Bayesian network accurately depicts causality, the two conditions are
# equivalent. However, a network may accurately embody the Markov condition without depicting
# causality, in which case it should not be assumed to embody the causal Markov condition.

# in_out is as defined above and input into this code.

if(checkMarkovDAG(in_out)$IsMarkovDAG & !checkMarkovDAG(in_out)$Reordered){
  print("Your in_out DAG is a Markov DAG.")
  } else if( checkMarkovDAG(in_out)$IsMarkovDAG & checkMarkovDAG(in_out)$Reordered ) {

      in_out <- checkMarkovDAG(in_out)[[2]]

          print("Your in_out DAG is a Markov DAG.The checkMarkovDAG function has reordered your
               in_out list so that all parent variables come before descendants.")
          } else{ print("Your ``in_out'' list is not a Bayesian Markov DAG so the methods in the
                        'causalPAF' package cannot be applied for non Markov DAGs.")}


# The pointEstimate() function evaluates Point Estimates for Total PAF, Direct PAF, Indirect PAF
# and Path Specific PAF for a user inputted number of integral simulations. There is no bootstrap
# applied in this function.
# Since bootstraps are not applied, the pointEstimate() function will run quicker than the
# alternative causalPAFplot() function which calculates bootstrap estimates which can take
# longer to run.


         pointEstimate(dataframe = stroke_reduced,
                       exposure="phys",
                       mediator=c("subhtn","apb","whr"),
                       response="case",
                       response_model_mediators = list(),
                       response_model_exposure = list(),
                       in_outArg = in_out,
                       Splines_outlist = Splines_outlist,
                       splinesDefinedIn_in_outDAG = TRUE,
                       model_listArg = list(),
                       weights = w,
                       NumSimulation = 3,
                       addCustom = TRUE,
                       custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)")


# The pointEstimate() function below has response_model_mediators, response_model_exposure and
# model_listArg pre fit. This allows the user to apply customised regressions instead of the
# default setting above, where the 'causalPAF' R package fitted these regressions automatically
# based on the causalDAG defined in in_outArg.

# Libraries must be loaded if fitting models outside of the 'causalPAF' R package.

library(MASS)
library(splines)


# Next we fit the, response_model_mediators and response_model_exposure, models outside of the
# 'causalPAF' package as an input into the package.

# It is important that response_vs_mediator is a list and it must be the same length as the
# parameter, mediator, i.e. length( response_vs_mediator ) == length( mediator). In this
# example, mediator=c("subhtn","apb","whr") so length( mediator) is 3, so we create a list
# with three models for "subhtn","apb" and "whr" respectively in that order. Note in this
# example, the model is the same for each mediator, but it must still be input 3 times within
# the list as follows:

response_vs_mediator <-  list(
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +subeduc+moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ),
# "subhtn" mediator model
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +  subeduc+ moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ),
# "apb" mediator model
glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5) +  subeduc+ moteduc+ fatduc+ phys+
ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2+ subhtn +
ns(apb, knots = quantile(apb,c(.25,0.5,0.75)),
Boundary.knots = quantile(apb,c(.001,0.95)))+
ns(whr,df=5)",data = stroke_reduced,family='binomial',w = stroke_reduced$weights ) )
 # "whr" mediator model


# Next we fit a customised response_model_exposure model rather than allowing the package fit it
# automatically as shown previously. This must be a list of length 1.
response_vs_phys <- list(glm("case ~ regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)+subeduc+moteduc+
fatduc+ phys+ ahei3tert+ nevfcur+ alcohfreqwk+ global_stress2",data = stroke_reduced,
family='binomial',w= stroke_reduced$weights) )

# model_listArg is a list of models fitted for each of the variables in in_out$outlist based on
# its parents given in in_out$inlist. By default this is set to an empty list. Alternatively the
# user can supply their custom fitted, model_listpop, which should be consistent with the causal
# structure. model_listArg is defined earlier in this tutorial.
# Note it is important that model_listArg is defined as a list and in the same order and length
# as the variables defined in in_outArg[[2]].

model_listArgFit <- list(glm(formula = phys ~ subeduc + regionnn7 * ns(eage, df = 5) +
esex * ns(eage, df = 5) + moteduc + fatduc, family = "binomial", data = stroke_reduced,
 weights = weights), # model 1 phys
polr(formula = ahei3tert ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, data = stroke_reduced, weights = weights), # model 2 ahei3tert
glm(formula = nevfcur ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, family = "binomial",data = stroke_reduced, weights = weights),
# model 3 nevfcur
polr(formula = alcohfreqwk ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc, data = stroke_reduced,weights = weights), # model 4 alcohfreqwk
glm(formula = global_stress2 ~ subeduc + regionnn7 * ns(eage,df = 5) + esex * ns(eage, df = 5) +
moteduc + fatduc, family = "binomial",data = stroke_reduced, weights = weights),
# model 5 global_stress2
glm(formula = subhtn ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2,family = "binomial",
data = stroke_reduced, weights = weights), # model 6 subhtn
lm(formula = apb ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2,
data = stroke_reduced,weights = weights), # model 7 apob_apoa coded as apb
lm(formula = whr ~ subeduc + regionnn7 * ns(eage, df = 5) + esex *ns(eage, df = 5) + moteduc +
fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2, data = stroke_reduced,
weights = weights), # model 8 whr
glm(formula = cardiacrfcat ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn,
family = "binomial",data = stroke_reduced, weights = weights), # model 9 cardiacrfcat
glm(formula = dmhba1c2 ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) +
moteduc + fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn,
family = "binomial",data = stroke_reduced, weights = weights), # model 10 dmhba1c2
glm(formula = case ~ subeduc + regionnn7 * ns(eage, df = 5) +esex * ns(eage, df = 5) + moteduc +
fatduc + phys + ahei3tert +nevfcur + alcohfreqwk + global_stress2 +
ns(apb, knots = quantile(apb,c(0.25, 0.5, 0.75)),
Boundary.knots = quantile(apb,c(0.001, 0.95))) + ns(whr, df = 5) + subhtn +
cardiacrfcat +dmhba1c2, family = "binomial", data = stroke_reduced, weights = weights)
# model 11 case
)


         pointEstimate(dataframe = stroke_reduced,
                       exposure="phys",
                       mediator=c("subhtn","apb","whr"),
                       response="case",
                       response_model_mediators = response_vs_mediator,
                       response_model_exposure = response_vs_phys,
                       in_outArg = in_out,
                       Splines_outlist = Splines_outlist,
                       splinesDefinedIn_in_outDAG = TRUE,
                       model_listArg = model_listArgFit,
                       weights = w,
                       NumSimulation = 3,
                       addCustom = TRUE,
                       custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)")



# See examples from the function causalPAFplot() to see how bootstraps and confidence intervals
# can be calculated in addition to the pont estimates calculated from the pointEstimate()
# function. The causalPAFplot() function also shows examples of plotting these point estimate
# results with confidence intervals.

Sequential Population Attributable Fractions in a Bayesian Network.

Description

'sequential_PAF' calculates and plots sequential population attributable fractions (PAF) under a Bayesian network structure.

Usage

sequential_PAF(
  dataframe,
  model_list_var,
  weights = 1,
  in_outDAG,
  response,
  NumOrderRiskFactors,
  addCustom = FALSE,
  custom = ""
)

Arguments

Details

Patients are listed in rows with variables (i.e. exposure, risk factors, confounders, outcome) listed in columns.

Value

Examples

# Loads some data (fictional Stroke data from the package 'causalPAF')
# In this example, we use a small data set called 'strokedata_smallSample' consisting of 5,000
# rows of fictional patient data. For more accurate results, a larger data set is available
# called 'strokedata'which contains 16,623 rows of fictional patient data. The methodology
# applied in the 'causalPAF' package is more accurate the larger the dataset. To use the larger
# 'strokedata' dataset, simply call
# stroke_reduced <- strokedata
stroke_reduced <- strokedata_smallSample

in_phys <- c("subeduc","moteduc","fatduc")
in_ahei <- c("subeduc","moteduc","fatduc")
in_nevfcur <- c("subeduc","moteduc","fatduc")
in_alcohfreqwk <- c("subeduc","moteduc","fatduc")
in_global_stress2 <- c("subeduc","moteduc","fatduc")
in_htnadmbp <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                 "global_stress2")
in_apob_apoatert <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                      "global_stress2")
in_whrs2tert <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2")
in_cardiacrfcat <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                     "global_stress2", "apob_apoatert","whrs2tert","htnadmbp")
in_dmhba1c2 <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
                  "global_stress2", "apob_apoatert","whrs2tert","htnadmbp")
in_case <- c("subeduc","moteduc","fatduc","phys","ahei3tert","nevfcur","alcohfreqwk",
"global_stress2", "apob_apoatert","whrs2tert","htnadmbp","cardiacrfcat","dmhba1c2")

in_out <- list(inlist=list(in_phys,in_ahei,in_nevfcur,in_alcohfreqwk,in_global_stress2,
               in_htnadmbp, in_apob_apoatert,in_whrs2tert,in_cardiacrfcat,
               in_dmhba1c2,in_case),
               outlist=c("phys","ahei3tert","nevfcur","alcohfreqwk","global_stress2",
                         "htnadmbp","apob_apoatert", "whrs2tert","cardiacrfcat",
                         "dmhba1c2","case"))



if(checkMarkovDAG(in_out)$IsMarkovDAG & !checkMarkovDAG(in_out)$Reordered){
  print("Your in_out DAG is a Markov DAG.")
} else if( checkMarkovDAG(in_out)$IsMarkovDAG & checkMarkovDAG(in_out)$Reordered ) {

  in_out <- checkMarkovDAG(in_out)[[2]]

  print("Your in_out DAG is a Markov DAG.The checkMarkovDAG function has reordered your
          in_out list so that all parent variables come before descendants.")
} else{ print("Your ``in_out'' list is not a Bayesian Markov DAG so the methods in the
               'causalPAF' package cannot be applied for non Markov DAGs.")}


w <- rep(1,nrow(stroke_reduced))
w[stroke_reduced$case==0] <- 0.9965
w[stroke_reduced$case==1] <- 0.0035

stroke_reduced$weights <- w

# 'NumOrderRiskFactors' should be set to a large number to ensure accurate results.
# This can take time to run.
sequentialPAF <- sequential_PAF( dataframe = stroke_reduced,
                                 model_list_var = list(),
                                 weights = w,
                                 in_outDAG = in_out,
                                 response = "case",
                                 NumOrderRiskFactors = 3,
                                 addCustom = TRUE,
                                 custom = "regionnn7*ns(eage,df=5)+esex*ns(eage,df=5)" )


sequentialPAF$SAF_summary


#######################################################################################
# Alternatively, the user can supply a customised model_list_var parameter as follows:
# Libraries must be loaded if fitting models outside of the 'causalPAF' R package.

library(MASS)
library(splines)


# model_list_var is a list of models fitted for each of the variables in in_outDAG$outlist based
# on its parents given in in_outDAG$inlist. By default this is set to an empty list.
# Alternatively the user can supply their custom fitted, model_list as follows, which should be
# consistent with the causal structure.
# Note it is important that model_listArg is defined as a list and in the same order and length
# as the variables defined in in_outDAG[[2]].


model_list <- list(
 glm(formula = phys ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) + moteduc
  + fatduc, family = "binomial", data = stroke_reduced, weights = weights), # model 1 phys
 polr(formula = ahei3tert ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc, data = stroke_reduced, weights = weights), # model 2 ahei3tert
 glm(formula = nevfcur ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc, family = "binomial",data = stroke_reduced, weights = weights), # model 3 nevfcur
 polr(formula = alcohfreqwk ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc, data = stroke_reduced,weights = weights), # model 4 alcohfreqwk
 glm(formula = global_stress2 ~ subeduc + regionnn7 * ns(eage,df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc, family = "binomial",data = stroke_reduced,
 weights = weights), # model 5 global_stress2
 glm(formula = htnadmbp ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2,
 family = "binomial",data = stroke_reduced, weights = weights), # model 6 htnadmbp
 polr(formula = apob_apoatert ~ regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 subeduc + moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2,
 data = stroke_reduced,weights = weights), # model 7 apob_apoatert
 polr(formula = whrs2tert ~ regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) + subeduc +
 moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2,
 data = stroke_reduced, weights = weights), # model 8 whrs2tert
 glm(formula = cardiacrfcat ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2 + apob_apoatert +
 whrs2tert + htnadmbp, family = "binomial",
 data = stroke_reduced, weights = weights), # model 9 cardiacrfcat
 glm(formula = dmhba1c2 ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2 + apob_apoatert +
 whrs2tert + htnadmbp, family = "binomial",
 data = stroke_reduced, weights = weights), # model 10 dmhba1c2
 glm(formula = case ~ subeduc + regionnn7 * ns(eage, df = 5) + esex * ns(eage, df = 5) +
 moteduc + fatduc + phys + ahei3tert + nevfcur + alcohfreqwk + global_stress2 + apob_apoatert +
 whrs2tert + htnadmbp + cardiacrfcat + dmhba1c2, family = "binomial", data = stroke_reduced,
 weights = weights) # model 11 case
 )


# 'NumOrderRiskFactors' should be set to a large number to ensure accurate results.
# This can take time to run.
 sequentialPAF <- sequential_PAF( dataframe = stroke_reduced,
                                  model_list_var = model_list,
                                  weights = stroke_reduced$weights,
                                  in_outDAG = in_out,
                                  response = "case",
                                  NumOrderRiskFactors = 3 )

sequentialPAF$SAF_summary

Set a variable defined in col_num to its reference level (or otherwise 0 i.e. symbolising the absence of the risk factor) and then simulate all it's children.

Description

Set variable defined in col_num to its reference level or otherwise to 0. Then simulate each variable if there is a direct arrow from the variable thats set to its reference value (or otherwise 0) to that variable i.e. if the variable set to its reference level (or otherwise 0) is a parent of a variable simulate the child.

Usage

sim_outnode(dataframe, col_num, current_mat, in_outArg, col_list, model_list)

Arguments

Value

Set a variable defined in col_num to its reference level (or otherwise 0 i.e. symbolising the absence of the risk factor) and then simulate all it's children.

Description

Set variable defined in col_num to its reference level or otherwise to 0. Then simulate each variable if there is a direct arrow from the variable thats set to its reference value (or otherwise 0) to that variable i.e. if the variable set to its reference level (or otherwise 0) is a parent of a variable simulate the child.

Usage

sim_outnode_2(
  dataframe,
  col_num,
  current_mat,
  col_list,
  model_list,
  response_col_num,
  in_outArg
)

Arguments

Value

Fictional ischemic stroke data case control data with risk factors, exposures and confounders

Description

A fictional standardized international study of ischemic stroke cases and controls in 32 countries in Asia, Europe, Australia, the Middle East and Africa. Information on key causal and modifiable risk factors for stroke are included. The risk factors included are healthy eating score (in tertiles), physical inactivity (yes/no), smoking behaviour (current smoker or ex/no smoker), alcohol intake (no alcohol, moderate consumption, high consumption), an indicator for stress, ApoB/ApoA lipid ratio (in tertiles), preexisting hypertension or high measured blood pressure (yes/no), waist hip ratio (in tertiles), cardiac risk factors such as atrial fibrillation or flutter (yes or no) and a diagnosis of diabetes mellitus or elevated HbA1c(yes/no). One needs to assume a causal graph describing the causal relationships between confounders, risk factors and disease to implement the methods in the 'causalPAF' package. To do this, it is helpful to divide the risk factors and exposures into categories depending on whether they are descriptive of an individual’s behaviour SB = Smoking, Alcohol intake, inactivity, diet and stress, their physiology SP = High blood pressure, ApoB/ApoA ratio, Waist hip ratio and what might be regarded as preclinical disease SD = Cardiac risk factors, Preclinical diabetes. We also consider a set of variables that might be confounders (joint causes of the risk factor and stroke) for all the listed risk factors. This set of confounders, SC consist of the individuals and their parents’ education level (in 5 levels from no education to holding a college Degree), age, gender and region. Here we make the simplifying assumption that disease develops in a stage wise fashion, each stage being represented by one of the sets of variables just described with variables in earlier stages having causal effects on variables contained in later stages, but not vice versa. The ordering of stages is indicated by the sequence, SC , SB , SP , SD , Y , and summarized by the causal graphs in (O’Connell and Ferguson 2020) <https://doi.org/10.1101/2020.10.15.20212845> and (Ferguson, O’Connell, and O’Donnell 2020) Revisiting sequential attributable fractions, J Ferguson, M O'Connell, M O'Donnell, Archives of Public Health, 2020.

Usage

strokedata

Format

A data frame with 16623 rows and 21 variables in columns. Each row representing either a fictional individual stroke case or control:

regionnn7

Region (number, 7 categories)

case

Case status (number, 1=cases, 0=controls)

esex

Gender (number, 1=female, 2=male)

eage

,Age based on both DOB and eage (number)

htnadmbp

High blood pressure, Hx HTN/Adjusted BP>140/90 at admission (number, 0=No, 1=Yes)

nevfcur

Smoke history(2lev) (number, 1=Never/Former, 2=Current)

global_stress2

Global Stress, (number, 1=None/some_periods, 2=Several/Perm. periods)

whrs2tert

Tertile of standing waist to hip ratio, WHR (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

phys

Leisure Physical activity (number, 1=mainly inactive, 2=mainly active)

alcohfreqwk

Alcohol history and frequency(3) (number, 1=Never/Former, 2=Low/Moderate, 3=High intake/Binge)

dmhba1c2

clinically diagnosed diabetes mellitus or measured Hba1c level at least 6.5 yes or no, Hx DM/HbA1c greater than or equal to 6.5 per cent (number, 1=No, 2=Yes)

cardiacrfcat

History of risk factors for heart disease yes or no, Hx Cardiac Risk Factors (number, 1=No, 2=Yes)

ahei3tert

Diet: AHEI diet score (in tertiles) Tertile of Total AHEI Score (not including alcohol), (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

apob_apoatert

Lipids: Apolipoprotein B/Apolipoprotein A1 ratio (in tertiles) (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

subeduc

Education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University)

moteduc

Mother education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University, 6=unknown)

fatduc

Father education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University, 6=Unknown)

subhtn

Blood pressure Hx HTN (number, 1=No, 2=Yes)

whr

Waist to hip ratio ( number as continuous variable)

apob_apoa

Lipids: Apolipoprotein B/Apolipoprotein A1 ratio (number as continuous variable)

weights

To fit these models to case control data, one needs to perform weighted maximum likelihood estimation to imitate estimation using a random sample from the population. We chose weights of 0.0035 (for each case) and 0.9965 (for each control), reflective of a yearly incidence of first ischemic stroke of 0.35 per cent, or 3.5 strokes per 1,000 individuals. These weights were chosen according to average incidences across country, age group and gender according to the global burden of disease.

Fictional ischemic stroke data case control data with risk factors, exposures and confounders

Description

A fictional standardized international study of ischemic stroke cases and controls in 32 countries in Asia, Europe, Australia, the Middle East and Africa. Information on key causal and modifiable risk factors for stroke are included. The risk factors included are healthy eating score (in tertiles), physical inactivity (yes/no), smoking behaviour (current smoker or ex/no smoker), alcohol intake (no alcohol, moderate consumption, high consumption), an indicator for stress, ApoB/ApoA lipid ratio (in tertiles), pre existing hypertension or high measured blood pressure (yes/no), waist hip ratio (in tertiles), cardiac risk factors such as atrial fibrillation or flutter (yes or no) and a diagnosis of diabetes mellitus or elevated HbA1c(yes/no). One needs to assume a causal graph describing the causal relationships between confounders, risk factors and disease to implement the methods in the 'causalPAF' package. To do this, it is helpful to divide the risk factors and exposures into categories depending on whether they are descriptive of an individual’s behaviour SB = Smoking, Alcohol intake, inactivity, diet and stress, their physiology SP = High blood pressure, ApoB/ApoA ratio, Waist hip ratio and what might be regarded as preclinical disease SD = Cardiac risk factors, Pre clinical diabetes. We also consider a set of variables that might be confounders (joint causes of the risk factor and stroke) for all the listed risk factors. This set of confounders, SC consist of the individuals and their parents’ education level (in 5 levels from no education to holding a college Degree), age, gender and region. Here we make the simplifying assumption that disease develops in a stage wise fashion, each stage being represented by one of the sets of variables just described with variables in earlier stages having causal effects on variables contained in later stages, but not vice versa. The ordering of stages is indicated by the sequence, SC , SB , SP , SD , Y , and summarized by the causal graphs in (O’Connell and Ferguson 2020) <https://doi.org/10.1101/2020.10.15.20212845> and (Ferguson, O’Connell, and O’Donnell 2020) Revisiting sequential attributable fractions, J Ferguson, M O'Connell, M O'Donnell, Archives of Public Health, 2020..

Usage

strokedata

Format

A data frame with 5000 rows and 21 variables in columns. Each row representing either a fictional individual stroke case or control:

regionnn7

Region (number, 7 categories)

case

Case status (number, 1=cases, 0=controls)

esex

Gender (number, 1=female, 2=male)

eage

,Age based on both DOB and eage (number)

htnadmbp

High blood pressure, Hx HTN/Adjusted BP>140/90 at admission (number, 0=No, 1=Yes)

nevfcur

Smoke history(2lev) (number, 1=Never/Former, 2=Current)

global_stress2

Global Stress, (number, 1=None/some_periods, 2=Several/Perm. periods)

whrs2tert

Tertile of standing waist to hip ratio, WHR (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

phys

Leisure Physical activity (number, 1=mainly inactive, 2=mainly active)

alcohfreqwk

Alcohol history and frequency(3) (number, 1=Never/Former, 2=Low/Moderate, 3=High intake/Binge)

dmhba1c2

clinically diagnosed diabetes mellitus or measured Hba1c level at least 6.5 yes or no, Hx DM/HbA1c greater than or equal to 6.5 per cent (number, 1=No, 2=Yes)

cardiacrfcat

History of risk factors for heart disease yes or no, Hx Cardiac Risk Factors (number, 1=No, 2=Yes)

ahei3tert

Diet: AHEI diet score (in tertiles) Tertile of Total AHEI Score (not including alcohol), (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

apob_apoatert

Lipids: Apolipoprotein B/Apolipoprotein A1 ratio (in tertiles) (number, 1=Tertile1, 2=Tertile2, 3=Tertile3)

subeduc

Education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University)

moteduc

Mother education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University, 6=unknown)

fatduc

Father education (number, 1=None, 2=1 to 8, 3=9 to 12, 4=Trade School, 5=College/University, 6=Unknown)

subhtn

Blood pressure Hx HTN (number, 1=No, 2=Yes)

whr

Waist to hip ratio ( number as continuous variable)

apob_apoa

Lipids: Apolipoprotein B/Apolipoprotein A1 ratio (number as continuous variable)

weights

To fit these models to case control data, one needs to perform weighted maximum likelihood estimation to imitate estimation using a random sample from the population. We chose weights of 0.0035 (for each case) and 0.9965 (for each control), reflective of a yearly incidence of first ischemic stroke of 0.35 per cent, or 3.5 strokes per 1,000 individuals. These weights were chosen according to average incidences across country, age group and gender according to the global burden of disease.